4.3 実験2の結果及び考察
4.3.1 結果の評価と分析方法
プラナリアは20℃で飼育すると10〜20日(平均15.9日)に1回、分裂することが知られている10)。また、一般的に生物の個体数が増加する初期段階では、指数的に増加することが知られている。そこで、それぞれの実験区の個体数の平均値から指数回帰曲線をもとめて、分裂頻度の違いについて比較検討した。その際、プラナリアが20日に1回分裂したとして、59日間のプラナリアの分裂回数は最低2回以上で、59日後のプラナリア個体数は4匹以上であると予想される。比較検討において、59日後のプラナリア個体数が全実験区で1匹(分裂なし)の場合は分裂が抑制されたと評価した。また、実験直前に分裂状態に入りつつある個体だったとすれば分裂1回(2匹)の実験区も実験水による分裂抑制があった可能性がある。そこで、59日後のプラナリア個体数が全実験区で2匹以下の場合も分裂が抑制されたと評価した。それ以外については、59日後のプラナリアの個体数(Table.12)をもとにt検定をおこない、分裂頻度に有為な差があるかを統計学的に検討した。
Table.12 各実験区59日後のプラナリアの個体数
| | 実験区(記号) | 1区 | 2区 | 3区 | 4区 | 5区 | 6区 | 平均 |
| 実験1 | 対照実験区 (C) | 5 | 3 | 4 | 5 | 3 | 3 | 3.8 |
| 実験2 | 対照実験区2 (CE) | 1 | 1 | 1 | 1 | 2 | 1 | 1.2 |
| 実験2 | スチレン実験区1 (M1) | 4 | 2 | 4 | 1 | 1 | 1 | 2.2 |
| 実験2 | スチレン実験区2 (M2) | 1 | 4 | 3 | 1 | 2 | 2 | 2.2 |
| 実験2 | ビスフェノールA実験区1(A1) | 1 | 1 | 1 | 1 | 1 | 1 | 1.0 |
| 実験2 | ビスフェノールA実験区2(A2) | 2 | 5 | 2 | 1 | 1 | 1 | 2.0 |
| 実験2 | ビスフェノールA実験区3(A3) | 1 | 2 | 1 | 1 | 2 | 3 | 1.7 |
t検定とはt分布を使って、2つの標本の母平均(母集団の平均)が等しいか等しくないかを確認する手法で、2グループ(標本数m、n)の分散が等しいときt値(平均の差を表す統計量)が自由度m+n−2のt分布に従うことを利用して検定する。一般的に、統計では標本数をある程度大きくして正規分布を利用するという、大標本理論に基づく計算がおこなわれる。しかし、個体や飼育条件の違いをなくし、同一条件での標本データを大量に収集することが困難である場合は、小標本理論に基づく計算がおこなわれる13,14)。Excelの分析ツールに用意されているt検定は、きわめて少ない標本でも2つの標本が、平均値の等しい母集団から取り出されたものであるかどうかを確率的に予測できる15)〜17)。そこで、t検定には表計算ソフトのExcel(Microsoft)をもちいた。
Excelのt検定の実行において仮説平均との差異は「0」を設定し、標本の平均が等しいことを帰無仮説として設定した。Excelのt検定の結果、tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却されるので、「2つの母集団平均は等しいとはいえない」ということになる。また、有意水準αの設定については、有意水準αを小さくしすぎると「帰無仮説が誤りであるのに受容してしまう確率」すなわち「第2種の誤り」を犯す確率を大きくしてしまうので、通例どおり0.05(信頼度95%)を有意水準αとした18)。(F検定も同様に設定した。)
Excelのt検定には「等分散を仮定した2標本による検定」と「分散が等しくないと仮定した2標本による検定」がある。このため2つの標本の平均値が等しいかどうかを調べるには、それぞれの標本の分散値に関する情報が必要となる。どの分析ツールを使用するかは、事前にF検定をおこない等分散性の検定をおこなった。
F検定はt検定と同様に表計算ソフトのExcel(Microsoft)をもちいた。ExcelのF検定で計算している内容は、「2つの標本の分散比が1にどれくらい近いか」ということであり、ExcelのF検定は両側検定だけが計算される「等分散性の検定」のための分析ツールである18)。したがって、ExcelのF検定の結果、分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却されるので、「不偏分散が大きい方の母分散は不偏分散が小さい方の母分散より大きい」ということになる18)。
4.3.2 スチレン実験区(M1,M2)
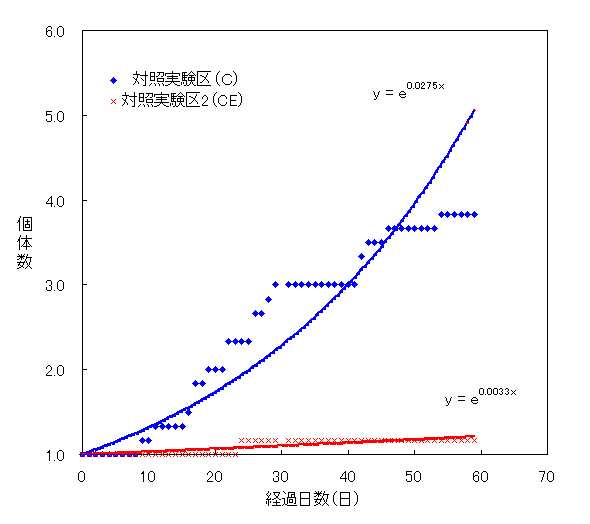
Fig.20 対照実験区(C、CE)におけるプラナリア個体数(平均値)の変化
Fig.20は対照実験区2(CE)と実験1の対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。yを個体数、xを経過日数とし、対照実験区(C)では y=e0.0275x 、対照実験区2(CE)ではy=e0.0033x となった。また、対照実験区2(CE)の59日後のプラナリア個体数は6区のうち1区が1回分裂しただけであった。したがって、対照実験区2(CE)においては明らかに分裂が抑制されていると考えられる。つまり、わずか1000ppbのエタノールが分裂を抑制していると考えられる。
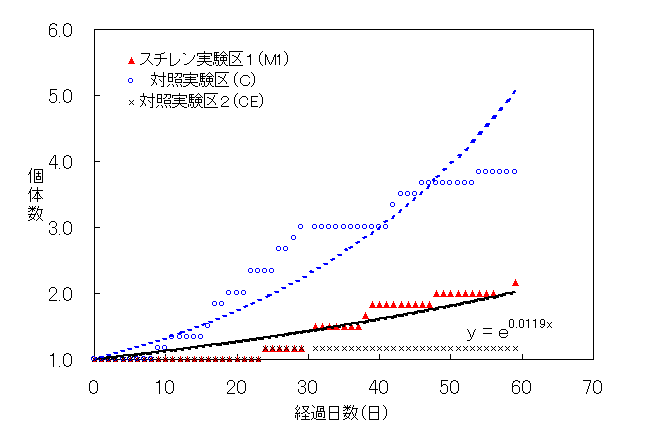
Fig.21 スチレン実験区1(M1)におけるプラナリア個体数(平均値)の変化
Fig.21は、スチレン実験区1(M1)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。yを個体数、xを経過日数とし、スチレン実験区1(M1)y=e0.0119x 、対照実験区(C)ではy=e0.0275x となった。また、スチレン実験区1の59日後のプラナリアの個体数は平均2.2匹であった。
このグラフの対照実験区(C)とスチレン実験区1(M1)の個体数増加の差が有為な差であるかを59日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:対照実験区の母分散とスチレン実験区1の母分散は等しい
対立仮説:対照実験区の母分散とスチレン実験区1の母分散は等しくない
Table.13は対照実験区(C)とスチレン実験区1(M1)のF検定の結果である。
Table.13 対照実験区Cとスチレン実験区1(M1)のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | M1(スチレン1ppb) | C(対照実験区) |
| 平均 | 2.167 | 3.833 |
| 分散 | 2.167 | 0.967 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 2.241 | |
| P(F<=f) 両側 | 0.198 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α0.05以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。Table.13では、P(F<=f) 両側
0.198は有意水準α0.05以上で、観測された分散比2.241はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:対照実験区の母平均とスチレン実験区1の母平均は等しい
対立仮説:対照実験区の母平均とスチレン実験区1の母平均は等しくない
となる。Table.14はt検定の結果である。
Table.14 対照実験区(C)とスチレン実験区1(M1)のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | C(対照実験区) | M1(スチレン1ppb) |
| 平均 | 3.833 | 2.167 |
| 分散 | 0.967 | 2.167 |
| 観測数 | 6 | 6 |
| プールされた分散 | 1.567 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 2.306 | |
| P(T<=t) 片側 | 0.022 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.044 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。計算の結果、P(T<=t) 両側0.044は有意水準α
0.05以下、t値2.306はt境界値両側2.228以上なので、帰無仮説は棄却され信頼度95%で2つの標本の母平均には有意な差があるといえる。
以上の結果から、対照実験区(C)とスチレン実験区1(M1)の個体数の増加、つまり分裂頻度には差があるといえる。
スチレン実験区1において、プラナリアの分裂頻度に影響を与えているのはスチレン
1ppbとエタノール1000ppbである。スチレン実験区1ではエタノール1000ppbのなかで分裂が抑制されるはずが、59日後のプラナリアの個体数は平均2.2匹であった。対照実験区2ではエタノールによって分裂が抑制されていたが、スチレン実験区1ではスチレン1ppbによって分裂頻度が1.2から2.2へ上昇したと考えられる。
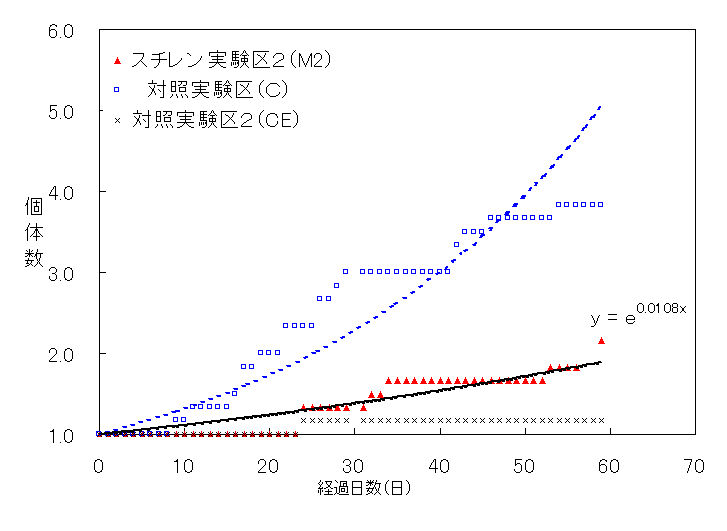
fig.22 スチレン実験区2(M2)におけるプラナリア個体数(平均値)の変化
Fig.22は、スチレン実験区2(M2)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。yを個体数、xを経過日数とし、スチレン実験区2(M2)y=e0.0108x 、対照実験区(C)ではy=e0.0275x となった。また、スチレン実験区2の59日後のプラナリアの個体数は平均2.2匹であった。そこで、対照実験区(C)とスチレン実験区2(M2)の個体数増加の差が有為な差であるかを
59日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:対照実験区の母分散とスチレン実験区2の母分散は等しい
対立仮説:対照実験区の母分散とスチレン実験区2の母分散は等しくない
Table.15は対照実験区(C)とスチレン実験区2(M2)のF検定の結果である。
Table.15 対照実験区(C)とスチレン実験区2(M2)のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | M2(スチレン0.01ppb) | C(対照実験区) |
| 平均 | 2.167 | 3.833 |
| 分散 | 1.367 | 0.967 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 1.414 | |
| P(F<=f) 両側 | 0.357 | |
| F 境界値 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.15では、P(F<=f) 両側0.357は有意水準α0.05以上で、観測された分散比1.414はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:対照実験区の母平均とスチレン実験区2の母平均は等しい
対立仮説:対照実験区の母平均とスチレン実験区2の母平均は等しくない
として、t検定をおこなった。Table.16はt検定の結果である。
Table.16 対照実験区(C)とスチレン実験区2(M2)のt検定の結果(Excel)
t-検定 : 等分散を仮定した2標本による検定 |
| C(対照実験区) | M2(スチレン0.01ppb) |
平均 | 3.833 | 2.167 |
分散 | 0.967 | 1.367 |
観測数 | 6 | 6 |
プールされた分散 | 1.167 | |
仮説平均との差異 | 0 | |
自由度 | 10 | |
t | 2.673 | |
P(T<=t) 片側 | 0.012 | |
t 境界値 片側 | 1.812 | |
P(T<=t) 両側 | 0.023 | |
t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。計算の結果、P(T<=t) 両側0.023は有意水準α
0.05以下、t値2.673はt境界値両側2.228以上なので、帰無仮説は棄却され信頼度95%で2つの標本の母平均には有意な差があるといえる。
以上の結果から、スチレン実験区2の59日後のプラナリアの個体数は平均2.2匹であったが、対照実験区(C)とスチレン実験区2(M2)の個体数の増加、つまり分裂頻度には差があるといえる。
スチレン実験区2においてプラナリアの分裂頻度にはスチレン0.0100ppbとエタノール
10ppbが影響を与えている。スチレン実験区1と同様に、濃度がM1の100分の1であるがエタノールが分裂を抑制し、濃度が100分の1のスチレンによって分裂を始めたと考えられる。つぎに、M1とM2のエタノールとスチレンの濃度の違いが分裂頻度にどのような違いを与えているかを比較検討した。
スチレン実験区におけるプラナリア個体数(平均値)の変化の比較
Fig.23のスチレン実験区1,2のプラナリア個体数(平均値)の変化を比較したグラフである。分裂開始時期はM1,M2ともに同じでスチレン濃度の影響を受けていない。また、点線で示したように38日目前後でM1とM2の分裂頻度が逆転している。前半スチレン濃度、エタノール濃度の低いM2の方が分裂頻度が高い。しかし、後半スチレン濃度、エタノール濃度の高いM1の方が分裂頻度が高くなっていく。これは、エタノールとスチレンの「分裂への作用」の違いであると考えられる。
エタノールの存在は分裂抑制として作用し、前半での分裂頻度の差はエタノールの濃度差によるものと考えられる。スチレンの作用は分裂抑制中から分裂頻度の上昇として作用し、後半での分裂頻度の差はスチレン濃度差によると考えられる。つまり、スチレンの作用は、遅れて現れる(遅効性)もので、発現までの期間は濃度の影響をうけず、スチレン濃度が高い方が分裂頻度が高まる。
また、次の点からスチレンにはホルモン作用があると考えられる。
・分裂抑制状態から分裂開始に移る時期が濃度差に関係なくM1、M2ともに同じであっ た。
・遅効性であった
・濃度差が後半に分裂促進作用として急激に発現した。
4.3.3 ビスフェノールA実験区(A1,A2,A3)
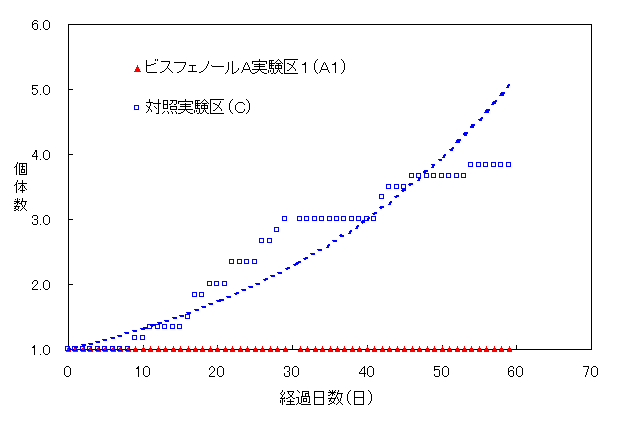
Fig.24 A1とCにおけるプラナリア個体数(平均値)の変化
Fig.24は、ビスフェノールA実験区1(A1)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。このグラフからは対照実験区(C)とビスフェノールA実験区1(A1)の個体数増加には明らかな差が認められる。ビスフェノールA実験区1(A1)の59日後のプラナリア個体数は6区すべてで分裂しなかった。したがって、ビスフェノールA2.00×103ppbによって分裂が抑制されたと考えられる。
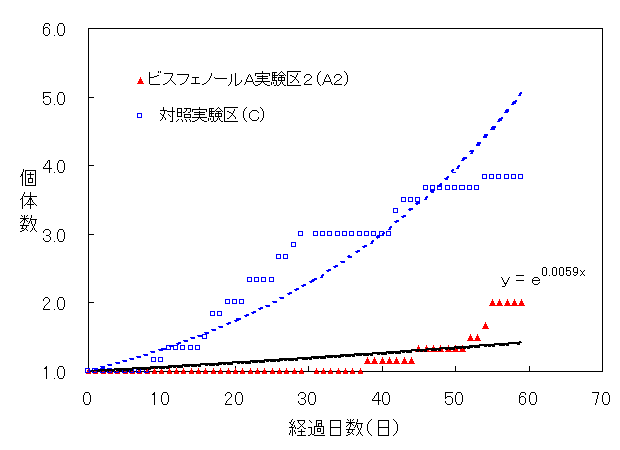
Fig.25 A2、Cにおけるプラナリア個体数(平均値)の変化
Fig.25は、ビスフェノールA実験区2(A2)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。yを個体数、xを経過日数とし、ビスフェノールA実験区2(A2)y=e0.0059x、対照実験区(C)ではy=e0.0129x となった。また、ビスフェノールA実験区2(A2)の59日後のプラナリアの個体数は平均2.0匹であった。このグラフの対照実験区(C)とビスフェノールA実験区2(A2)の個体数増加の差が有為な差であるかを59日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:対照実験区の母分散とビスフェノールA実験区2の母分散は等しい
対立仮説:対照実験区の母分散とビスフェノールA実験区2の母分散は等しくない
Table.18は対照実験区(C)とビスフェノールA実験区2(A2)のF検定の結果である。
Table.18 対照実験区(C)と
ビスフェノールA実験区2(A2)のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | A2(ビスフェノールA 5ppb) | C(対照実験区) |
| 平均 | 2.000 | 3.833 |
| 分散 | 2.400 | 0.967 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 2.483 | |
| P(F<=f) 両側 | 0.170 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.18では、P(F<=f) 両側0.170は有意水準α以上で、観測された分散比2.483はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:対照区の母平均と実験区の母平均は等しい
対立仮説:対照区の母平均と実験区の母平均は等しくない
として、t検定をおこなった。Table.19はt検定の結果である。
Table.19 対照実験区(C)と
ビスフェノールA実験区2(A2)のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | C(対照実験区) | A2(ビスフェノールA 5ppb) |
| 平均 | 3.833 | 2.000 |
| 分散 | 0.967 | 2.400 |
| 観測数 | 6 | 6 |
| プールされた分散 | 1.683 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 2.447 | |
| P(T<=t) 片側 | 0.017 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.034 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。計算の結果、P(T<=t) 両側0.034は有意水準α
0.05以下であるが、t値2.447はt境界値両側2.228以上なので、帰無仮説は棄却され信頼度95%で2つの標本の母平均には有意な差があるといえる。
以上の結果から、対照実験区(C)とビスフェノールA実験区2(A2)の個体数の増加、つまり分裂頻度には差があるといえる。ビスフェノールA実験区2(A2)においてプラナリアの分裂頻度に影響を与えているのはビスフェノールA5.00ppbである。ビスフェノールA実験区1(A1)では59日間分裂しなかったが、ビスフェノールA実験区2(A2)では、38日目から分裂が始まっている。ビスフェノールA濃度が2000ppbから
5.00ppbに減少したことによって分裂が始まったと考えられる。
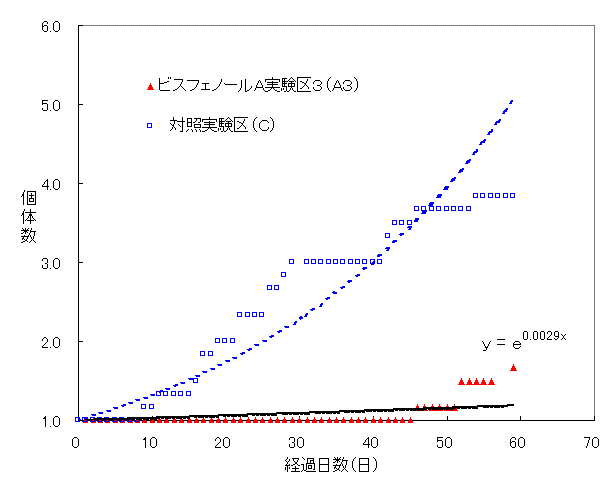
Fig.27 ビスフェノールA実験区3におけるプラナリア個体数(平均値)の変化
Fig.27は、ビスフェノールA実験区3(A3)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。yを個体数、xを経過日数とし、ビスフェノールA実験区3(A3)y=e0.0029x、対照実験区(C)ではy=e0.0129x となった。また、ビスフェノールA実験区3(A3)の59日後のプラナリアの個体数は平均1.7匹であった。このグラフの対照実験区(C)とビスフェノールA実験区3
(A3)の個体数増加の差が有為な差であるかを59日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:対照区の母分散と実験区の母分散は等しい
対立仮説:対照区の母分散と実験区の母分散は等しくない
Table.20は対照実験区(C)とビスフェノールA実験区3(A3)のF検定の結果である。
Table.20 ビスフェノールA実験区3(A3)と対照実験区(C)のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | C(対照実験区) | A3(ビスフェノールA 0.05ppb) |
| 平均 | 3.833 | 1.667 |
| 分散 | 0.967 | 0.667 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 1.450 | |
| P(F<=f) 両側 | 0.347 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.20では、P(F<=f) 両側0.347は有意水準α0.05以上で、観測された分散比1.450はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:対照区の母平均と実験区の母平均は等しい
対立仮説:対照区の母平均と実験区の母平均は等しくない
として、t検定をおこなった。Table.21はt検定の結果である。
Table.21 対照実験区(C)と
ビスフェノールA実験区3(A3)のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | C(対照実験区) | A3(ビスフェノールA 0.05ppb) |
| 平均 | 3.833 | 1.667 |
| 分散 | 0.967 | 0.667 |
| 観測数 | 6 | 6 |
| プールされた分散 | 0.817 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 4.153 | |
| P(T<=t) 片側 | 0.001 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.002 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。計算の結果、P(T<=t) 両側0.002は有意水準α
0.05以下、t値4.153はt境界値両側2.228以上なので、帰無仮説は棄却され信頼度95%で2つの標本の母平均には有意な差があるといえる。
以上の結果から、対照実験区(C)とビスフェノールA実験区3(A3)の個体数の増加、つまり分裂頻度には差があるといえる。ビスフェノールA実験区3(A3)においてプラナリアの分裂頻度に影響を与えているのはビスフェノールA0.05ppbである。ビスフェノールA実験区1(A1)では59日間分裂しなかったが、ビスフェノールA実験区3(A3)では、45日目から分裂が始まっている。ビスフェノールA濃度が2000ppbから
0.05ppbに減少したことによって分裂が始まったと考えられる。
では、ビスフェノールA実験区2(A2)とビスフェノールA実験区3(A3)には濃度による分裂頻度の差が生じているのだろうか。この点を確認するため59日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:A2の母分散とA3の母分散は等しい
対立仮説:A2の母分散とA3の母分散は等しくない
Table.22はビスフェノールA実験区2,3のF検定の結果である。
Table.22 ビスフェノールA実験区2,3のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | A2(ビスフェノールA 5ppb) | A3(ビスフェノールA 0.05ppb) |
| 平均 | 2.000 | 1.667 |
| 分散 | 2.400 | 0.667 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 3.600 | |
| P(F<=f) 両側 | 0.093 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.22では、P(F<=f) 両側0.093は有意水準α0.05以上で、観測された分散比3.600はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:A2の母平均とA3の母平均は等しい
対立仮説:A2の母平均とA3の母平均は等しくない
として、t検定をおこなった。Table.23はt検定の結果である。
Table.23 ビスフェノールA実験区2,3のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | A2(ビスフェノールA 5ppb) | A3(ビスフェノールA 0.05ppb) |
| 平均 | 2.000 | 1.667 |
| 分散 | 2.400 | 0.667 |
| 観測数 | 6 | 6 |
| プールされた分散 | 1.533 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 0.466 | |
| P(T<=t) 片側 | 0.326 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.651 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。
計算の結果、P(T<=t) 両側0.651は有意水準α0.05以上、t値0.466はt境界値両側 2.228以内なので、帰無仮説は受容され信頼度95%で2つの標本の母平均には有意な差がないといえる。
以上の結果から、ビスフェノールA実験区2(A2)とビスフェノールA実験区3
(A3)の個体数の増加、つまり分裂頻度には差がないといえる。よって、5ppbと0.05
ppbの濃度差はプラナリアの分裂頻度に大きな影響を与えていないと考えられる。
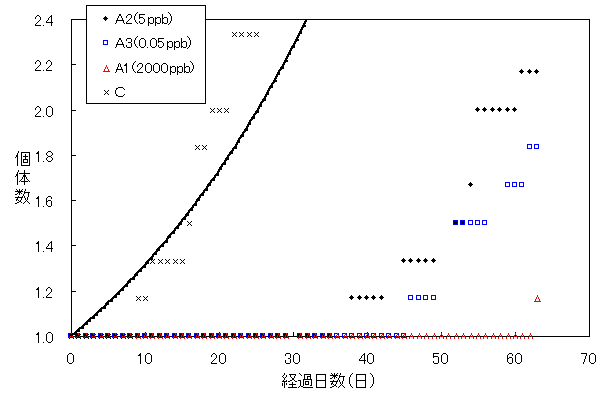
Fig.28 ビスフェノールA実験区におけるプラナリア個体数(平均値)の変化
Fig.28は、ビスフェノールA実験区1,2,3(A1、A2、A3)と対照実験区(C)におけるプラナリア個体数の平均値と経過日数の関係をグラフにしたものである。
このグラフから対照実験区(C)に比べ、A1、A2、A3は分裂開始が遅れていることが分かる。また、A2、A3のグラフの立ち上がり方は対照実験区(C)に似ている。そこで、各実験区の分裂開始前日を1日目として経過日数を調整したグラフを作成し、各実験区の指数回帰曲線をもとめて、分裂頻度の違いについて再度比較検討した。Fig.29は経過日数調整後のグラフである。また、比較検討には、調整後の32日目の個体数の平均値をもとにt検定をおこなった。
Table.24は調整後の32日目の個体数の平均値である。
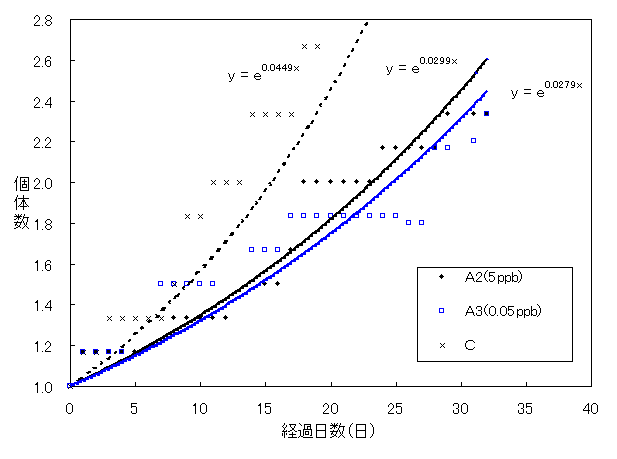
Fig.29 分裂開始を1日目としたプラナリア個体数(平均値)の変化
Table.24 分裂開始を1日目とした32日目のプラナリアの個体数
| | 実験区(記号) | 1区 | 2区 | 3区 | 4区 | 5区 | 6区 | 平均 |
| 実験1 | 対照実験区 (C) | 3 | 3 | 2 | 5 | 2 | 3 | 3.0 |
| 実験2 | ビスフェノールA実験区2(A2) | 4 | 5 | 3 | 1 | 1 | 1 | 2.5 |
| 実験2 | ビスフェノールA実験区3(A3) | 1 | 6 | 1 | 1 | 3 | 2 | 2.3 |
まず、分裂開始を1日目としたプラナリアの個体数について、対照実験区(C)とビスフェノールA実験区2(A2)の個体数増加の差が有為な差であるかを32日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:調整後Cの母分散と調整後A2の母分散は等しい
対立仮説:調整後Cの母分散と調整後A2の母分散は等しくない
Table.25は分裂開始を1日目とした対照実験区(C)とビスフェノールA実験区2
(A2)のF検定の結果である。
Table.25 分裂開始を1日目としたCとA2のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | A2(ビスフェノールA 5ppb) | C(対照実験区) |
| 平均 | 2.500 | 3.000 |
| 分散 | 3.100 | 1.200 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 2.583 | |
| P(F<=f) 両側 | 0.160 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.25では、P(F<=f) 両側0.160 は有意水準α0.05以上で、観測された分散比
2.583 はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:調整後Cの母平均と調整後A2の母平均は等しい
対立仮説:調整後Cの母平均と調整後A2の母平均は等しくない
として、t検定をおこなった。Table.26はt検定の結果である。
Table.26 分裂開始を1日目としたCとA2のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | C(対照実験区) | A2(ビスフェノールA 5ppb) |
| 平均 | 3.000 | 2.500 |
| 分散 | 1.200 | 3.100 |
| 観測数 | 6 | 6 |
| プールされた分散 | 2.150 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 0.591 | |
| P(T<=t) 片側 | 0.284 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.568 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。
計算の結果、P(T<=t) 両側0.568は有意水準α0.05以上、t値1.812はt境界値両側
2.228以内なので、帰無仮説は受容され信頼度95%で2つの標本の母平均には有意な差がないといえる。
以上の結果から、分裂開始を1日目とした対照実験区(C)とビスフェノールA実験区2(A2)の個体数の増加、つまり分裂頻度には差がないといえる。
つぎに、分裂開始を1日目とした対照実験区(C)とビスフェノールA実験区3(A3)の個体数増加の差が有為な差であるかを32日後のプラナリアの個体数をもとにt検定をおこない統計学的に検討した。
F検定は、有意水準αを0.05、両側検定をExcelでおこなった。
帰無仮説:調整後Cの母分散とビスフェノールA実験区3の母分散は等しい
対立仮説:調整後Cの母分散とビスフェノールA実験区3の母分散は等しくない
Table.27は調整後の対照実験区(C)とビスフェノールA実験区3(A3)のF検定の結果である。
Table.27 分裂開始を1日目としたCとA3のF検定の結果(Excel)
| F-検定 : 2 標本を使った分散の検定 |
| | A3(ビスフェノールA 0.05ppb) | C(対照実験区) |
| 平均 | 2.333 | 3.000 |
| 分散 | 3.867 | 1.200 |
| 観測数 | 6 | 6 |
| 自由度 | 5 | 5 |
| 観測された分散比 | 3.222 | |
| P(F<=f) 両側 | 0.112 | |
| F 境界値 両側 | 5.050 | |
分散比が1以上の場合、P(F<=f) 両側が有意水準α以下であるか、あるいは分散比がF境界値両側以上ならば、帰無仮説は棄却される18)。
Table.26では、P(F<=f) 両側0.112は有意水準α0.05以上で、観測された分散比3.222はF境界値両側5.050以内なので、帰無仮説は受容される。よって、信頼度95%で、等分散である。
つぎに、Excelでt検定(等分散を仮定した2標本による検定)をおこなった。t検定では、仮説平均との差異を0、有意水準αを0.05として、両側検定をおこなった。仮説平均との差異0と設定したので、
帰無仮説:調整後Cの母平均と調整後A3の母平均は等しい 対立仮説:調整後Cの母平均と調整後A3の母平均は等しくない
として、t検定をおこなった。Table.28はt検定の結果である。
Table.28 分裂開始を1日目としたCとA3のt検定の結果(Excel)
| t-検定 : 等分散を仮定した2標本による検定 |
| | C(対照実験区) | A3(ビスフェノールA 0.05ppb) |
| 平均 | 3.000 | 2.333 |
| 分散 | 1.200 | 3.867 |
| 観測数 | 6 | 6 |
| プールされた分散 | 2.533 | |
| 仮説平均との差異 | 0 | |
| 自由度 | 10 | |
| t | 0.725 | |
| P(T<=t) 片側 | 0.242 | |
| t 境界値 片側 | 1.812 | |
| P(T<=t) 両側 | 0.485 | |
| t 境界値 両側 | 2.228 | |
tが正の場合、P(T<=t) 両側が有意水準α以下であるか、あるいはt値がt境界値両側以上ならば、帰無仮説は棄却される。
計算の結果、P(T<=t) 両側0.485は有意水準α0.05以上、t値0.725はt境界値両側
2.228以内なので、帰無仮説は受容され信頼度95%で2つの標本の母平均には有意な差がないといえる。
以上の結果から、分裂開始を1日目とした対照実験区(C)とビスフェノールA実験区3(A3)の個体数の増加、つまり分裂頻度には差がないといえる。
調整後、対照実験区(C)とビスフェノールA実験区2,3の分裂頻度には差がなくなった。以上の結果から、ビスフェノールAには分裂開始時期を遅らせるだけの働きがあると考えられる。また、分裂開始時期を遅らせる作用と濃度との関係は、
A1(2.00ppm)62日>A3(0.050ppb)45日>A2(5.0ppb)35日
となり、はっきりとした傾向は見いだされなかった。
4.4 実験2の結論
・スチレンにはホルモン作用があり、エタノールによって抑制された分裂を促進する働き がある。
・スチレンの働きが発現するまでの期間は、濃度の影響をうけない。
・ビスフェノールAには分裂開始時期を遅らせる働きがある。








